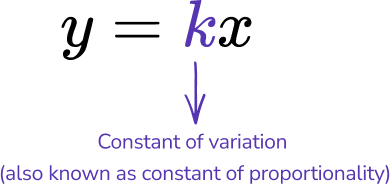
Here you will learn about direct variation, including the constant of variation, the equation that represents direct variation, and interpreting the graphs of direct variation.
Students first learn about proportional relationships on a graph in the 6th grade with ratio tables in ratios and proportional relationships.
Direct variation is a proportional relationship between the x -coordinate (an independent variable) and the y -coordinate (a dependent variable), where the ratio between the x -coordinate and the y -coordinate is constant.
Direct variation is represented algebraically by the equation,
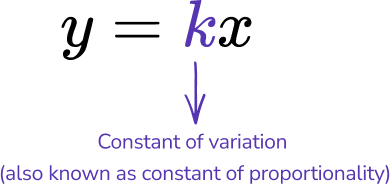
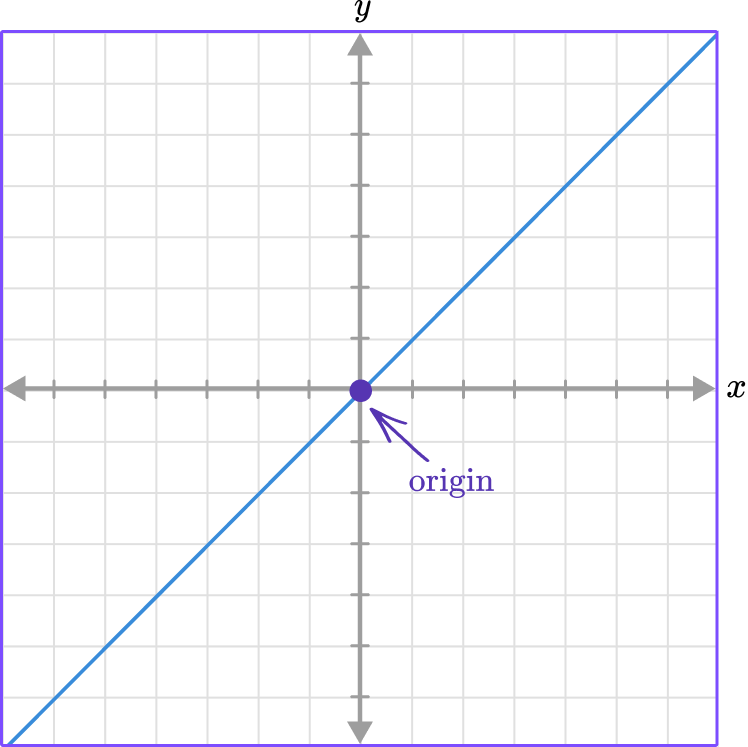
Direct variation is represented graphically by a line that goes through the origin.
Let’s look at some examples,
The equation y=\cfrac \, x represents direct variation. What is the constant of variation?
The constant of variation is represented by k in the equation y=kx.
So in this case, \, \cfrac \, is the constant of variation.
You can use a graph to determine the constant of variation.
For example, use the graph to find the constant of variation.
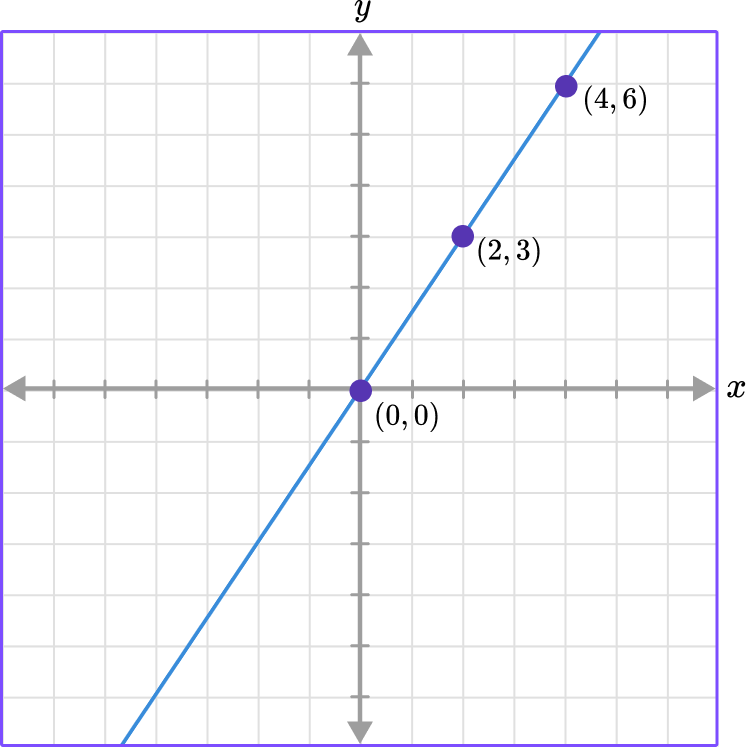
The line goes through the origin and also contains the points of (2, 3) and (4, 6).
To find the constant of variation or the constant of proportionality you can write the ratio of the points in the form of \, \cfrac \, because k=\cfrac .
Choosing the point (2, 3) the ratio is \, \cfrac \, which means that k=\cfrac .
The constant of variation, k, can also be found by counting the units from one point to the next. You can see that from (0, 0) to (2, 3) you moved to the right 2 units and up 3 units, and from points (2, 3) to (4, 6) the same movement occurred.
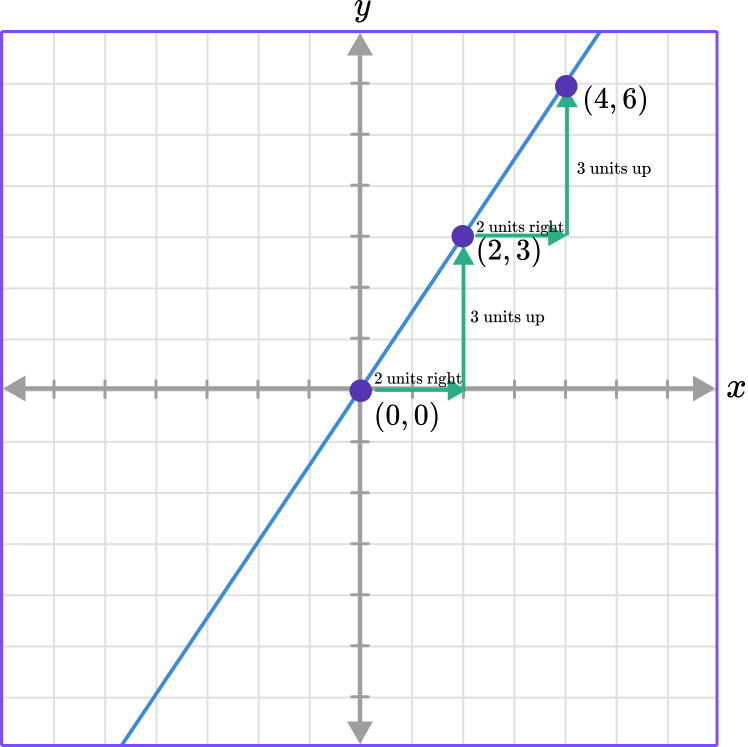
The constant movement from one point to the next is also called the constant rate of change.