

Imagine a mechanic turning a wrench to tighten a bolt. The mechanic applies a force at the end of the wrench. This creates rotation, or torque, which tightens the bolt. We can use vectors to represent the force applied by the mechanic, and the distance (radius) from the bolt to the end of the wrench. Then, we can represent torque by a vector oriented along the axis of rotation. Note that the torque vector is orthogonal to both the force vector and the radius vector.
In this section, we develop an operation called the cross product, which allows us to find a vector orthogonal to two given vectors. Calculating torque is an important application of cross products, and we examine torque in more detail later in the section.
The dot product is a multiplication of two vectors that results in a scalar. In this section, we introduce a product of two vectors that generates a third vector orthogonal to the first two. Consider how we might find such a vector. Let \(\vecs u=⟨u_1,u_2,u_3⟩\) and \(\vecs v=⟨v_1,v_2,v_3⟩\) be nonzero vectors. We want to find a vector \(\vecs w=⟨w_1,w_2,w_3⟩\) orthogonal to both \(\vecs u\) and \(\vecs v\)—that is, we want to find \(\vecs w\) such that \(\vecs u ⋅ \vecs w=0\) and \( \vecs v⋅ \vecs w=0\). Therefore, \(w_1\), \(w_2,\) and \(w_3\) must satisfy
If we multiply the top equation by \(v_3\) and the bottom equation by \(u_3\) and subtract, we can eliminate the variable \(w_3\), which gives
\[\begin w_1 &=u_2v_3−u_3v_2 \\[4pt] w_2 &=−(u_1v_3−u_3v_1), \end\]
we get a possible solution vector. Substituting these values back into the original equations (Equations \ref and \ref) gives
\[\vecs w=⟨u_2v_3−u_3v_2,−(u_1v_3−u_3v_1),u_1v_2−u_2v_1⟩ \nonumber \]
is orthogonal to both \(\vecs u\) and \(\vecs v\), which leads us to define the following operation, called the cross product.
Let \(\vecs u=⟨u_1,u_2,u_3⟩\) and \(\vecs v=⟨v_1,v_2,v_3⟩.\) Then, the cross product \(\vecs u×\vecs v\) is vector
\[\begin \vecs u×\vecs v &= (u_2v_3−u_3v_2)\mathbf<\hat i>−(u_1v_3−u_3v_1) \mathbf<\hat j>+(u_1v_2−u_2v_1)\mathbf <\hat k>\nonumber \\[4pt] &=⟨u_2v_3−u_3v_2,−(u_1v_3−u_3v_1),u_1v_2−u_2v_1⟩. \label\end \]
From the way we have developed \(\vecs u×\vecs v\), it should be clear that the cross product is orthogonal to both \(\vecs u\) and \(\vecs v\). However, it never hurts to check. To show that \(\vecs u×\vecs v\) is orthogonal to \(\vecs u\), we calculate the dot product of \(\vecs u\) and \(\vecs u×\vecs v\).
\[\begin \vecs u⋅(\vecs u×\vecs v) &=⟨u_1,u_2,u_3⟩⋅⟨u_2v_3−u_3v_2,−u_1v_3+u_3v_1,u_1v_2−u_2v_1⟩ \\[4pt] &=u_1(u_2v_3−u_3v_2)+u_2(−u_1v_3+u_3v_1)+u_3(u_1v_2−u_2v_1) \\[4pt]
&=u_1u_2v_3−u_1u_3v_2−u_1u_2v_3+u_2u_3v_1+u_1u_3v_2−u_2u_3v_1\\[4pt]
&=(u_1u_2v_3−u_1u_2v_3)+(−u_1u_3v_2+u_1u_3v_2)+(u_2u_3v_1−u_2u_3v_1) \\[4pt]
&= 0 \end\]
In a similar manner, we can show that the cross product is also orthogonal to \(\vecs v\).
Let \(\vecs p=⟨−1,2,5⟩\) and \(\vecs q=⟨4,0,−3⟩\) (Figure \(\PageIndex\)). Find \(\vecs p×\vecs q\).
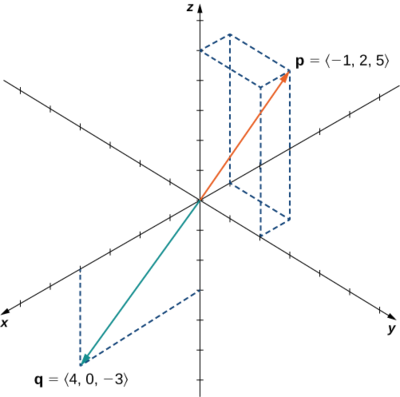
Substitute the components of the vectors into Equation \ref:
\[\begin \vecs p×\vecs q &=⟨−1,2,5⟩×⟨4,0,−3⟩ \\[4pt] &= ⟨p_2q_3−p_3q_2,-(p_1q_3−p_3q_1),p_1q_2−p_2q_1⟩ \\[4pt] &= ⟨2(−3)−5(0),−(−1)(−3)+5(4),(−1)(0)−2(4)⟩ \\[4pt] &= ⟨−6,17,−8⟩.\end\]
Find \(\vecs p×\vecs q\) for \(\vecs p=⟨5,1,2⟩\) and \(\vecs q=⟨−2,0,1⟩.\) Express the answer using standard unit vectors.
Hint
Use the formula \(\vecs u×\vecs v=(u_2v_3−u_3v_2)\mathbf<\hat i>−(u_1v_3−u_3v_1)\mathbf<\hat j>+(u_1v_2−u_2v_1)\mathbf<\hat k>.\)
Answer
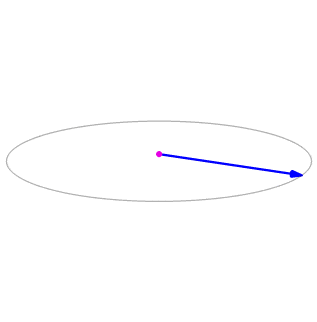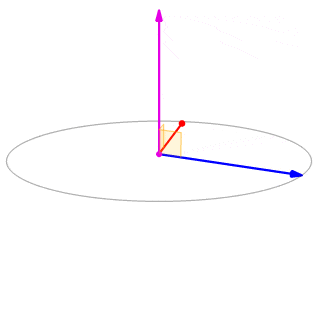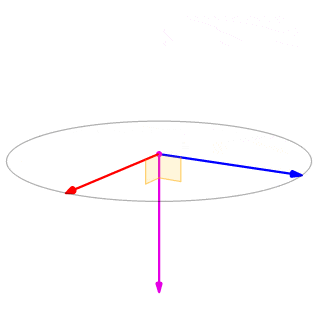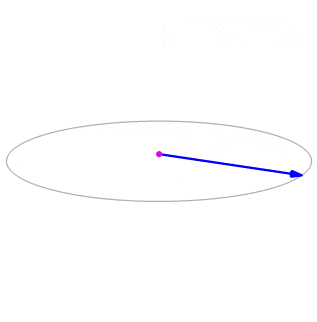
Although it may not be obvious from Equation \ref, the direction of \(\vecs u×\vecs v\) is given by the right-hand rule. If we hold the right hand out with the fingers pointing in the direction of \(\vecs u\), then curl the fingers toward vector \(\vecs v\), the thumb points in the direction of the cross product, as shown in Figure \(\PageIndex\).
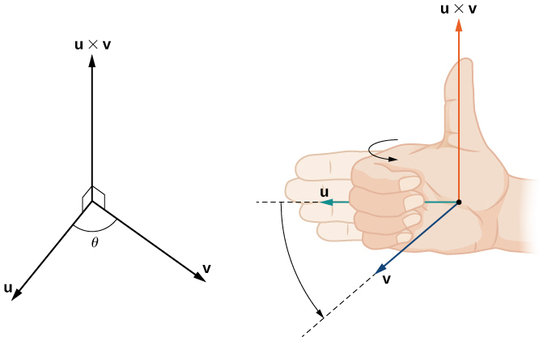
Notice what this means for the direction of \(\vecs v×\vecs u\). If we apply the right-hand rule to \(\vecs v×\vecs u\), we start with our fingers pointed in the direction of \(\vecs v\), then curl our fingers toward the vector \(\vecs u\). In this case, the thumb points in the opposite direction of \(\vecs u×\vecs v\). (Try it!)
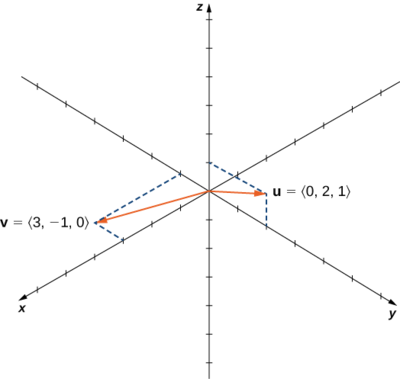
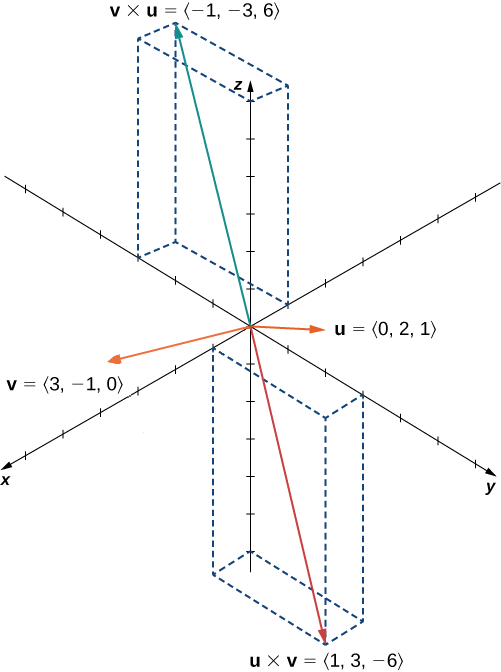
Let \(\vecs u=⟨0,2,1⟩\) and \(\vecs v=⟨3,−1,0⟩\). Calculate \(\vecs u×\vecs v\) and \(\vecs v×\vecs u\) and graph them.
We see that, in this case, \(\vecs u×\vecs v=−(\vecs v×\vecs u)\) (Figure \(\PageIndex\)). We prove this in general later in this section.
Suppose vectors \(\vecs u\) and \(\vecs v\) lie in the \(xy\)-plane (the \(z\)-component of each vector is zero). Now suppose the \(x\)- and \(y\)-components of \(\vecs u\) and the \(y\)-component of \(\vecs v\) are all positive, whereas the \(x\)-component of \(\vecs v\) is negative. Assuming the coordinate axes are oriented in the usual positions, in which direction does \(\vecs u×\vecs v\) point?
Hint
Remember the right-hand rule (Figure \(\PageIndex\)).
Answer
Up (the positive \(z\)-direction)
The cross products of the standard unit vectors \(\mathbf<\hat i>\), \(\mathbf<\hat j>\), and \(\mathbf<\hat k>\) can be useful for simplifying some calculations, so let’s consider these cross products. A straightforward application of the definition shows that
(The cross product of two vectors is a vector, so each of these products results in the zero vector, not the scalar \(0\).) It’s up to you to verify the calculations on your own.
Furthermore, because the cross product of two vectors is orthogonal to each of these vectors, we know that the cross product of \(\mathbf<\hat i>\) and \(\mathbf<\hat j>\) is parallel to \(\mathbf<\hat k>\). Similarly, the vector product of \(\mathbf<\hat i>\) and \(\mathbf<\hat k>\) is parallel to \(\mathbf<\hat j>\), and the vector product of \(\mathbf<\hat j>\) and \(\mathbf<\hat k>\) is parallel to \(\mathbf<\hat i>\).
We can use the right-hand rule to determine the direction of each product. Then we have
These formulas come in handy later.